Задание 3.

Задачи на равномерное движение.

Цель:
-научиться правильно работать с графиками.
-научиться решать задачи на равномерное движение.
-уметь определять координаты движения тел
-составлять уравнения равномерного движения.




Задача 1.
Опишите, как движется мистр Джонс, если уравнение его движения х=-4+10t. Найдите начальную координату его движения и направление скорости. Постройте график х(t).

решение: 

x=x0+Vxt
x0=-4
Vx=10 м/с
x=-4+10t
  Найдём в какой момент времени Мистер  Джонс будет проходить дом.
xa=8
 ta -?
           8=-4+10t
          10t=12
           t=1,2(с)

Ответ:
x=-4+10t
 ta=1,2 сек.

 Задача 2.
 Мистер Джонс и его коллега по работе решили встретиться . Они идут навстречу друг к другу. Написать уравнения движения тел, характер движения. Начертите график Vх(t). Найдите место и время встречи.

Решение. 


1 тело:                                                 2 тело:
х0= 54                                                 Х0=60
Vх=х-х0/t                                              Vх=х-х0/t
Vх=0-54/6=- 9                                   Vх=0-60/2=-30
х=54-9t                                                  х=60-30t 

 Встреча: х1=х2


54-9t= 60-30t   
-9t+30t= -54+60
21t=6
t=6\21
t= 0,28
x= 60 -30 *0,28= 60-8,4=51,6


Задача 3.
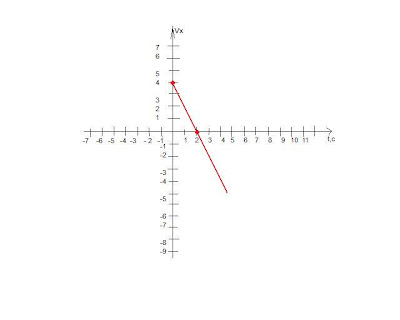
Уравнение движения мистера Джонса задано уравнением х=4-2t. Определите начальную координату и направление скорости. Постройте график Vх(t);

X0=4
Vx=-2 

              "Определение проэкции вектора на оси".

Работа №2.
Вариант № 4.

Цель:

• Опроделить координаты начала и конца каждого вектора.
• Определить проекции векторов на оси.
• Определить длину векторов.
• Определить сумму и разность двух предложенных векторов.

                  Результаты вычисления:

 Вектор АВ:

Начальные координаты:                        Конечные координаты:

  x0= 1                                                                    x=9

  y0=  4                                                                   y= 2

                                    Проекции векторов:
                        Sx=x-x0                                Sy=y-y0    

  Sx= 9-1=8             Sy=2-4=-2

                                      Длина вектора AB:
   |S^2| =Sx^2+Sy^2 

   |S^2| = 64+4=70

Вектор CD:
Начальные координаты:                      Конечные координаты:    x0=13                                                                       x=9
    y0= 4                                                                        y= 8

                                Проекции векторов:
            Sx=x-x0                                                Sy=y-y0     

           Sx= 9-13=-4                                         Sy= 8-4=4

                                      Длина вектора CD: 

  |S^2|=Sx^2+Sy^2

  |S^2|=16+16=32

 Переместим векторы так, чтобы начальная точка CD лежала в конечной точке AB:
AB+CD=AD

Вектор AD

A(2;4)

D( 9;2)

 

 Sx=x-x0                Sy=y-y0

  Sx= 9-2=7             Sy= 2-4=-2

 |AD^2|=Sx^2+Sy^2

 |AD^2|= 49+4= 53

 |AD|= 53

                                      Разность AB-CD:
Переместим векторы так, чтобы оба вектора AB и CD выходили из одной точки:
AB-CD=BD
Вектор BD 

B(9;2)

D( -3;7)

 Sx=x-x0                            Sy=y-y0 

  Sx= -3-9=-12                     Sy= 7-2=5

BD^2=Sx^2+Sy^2
|BD^2|= 144+25=169

BD=13 

 

https://docs.google.com/document/d/1LJNsttPQeJn3XJO4rLMPjHtVLHAFRCh5VLrR9Z5wBCk/edit?hl=en_US